선형 회귀 (Linear Regression)

#1. 개념

1-1. 정의

  선형 회귀는 지도학습의 한 종류로, 독립 변수(X)와 종속 변수(Y) 간의 선형 관계를 모델링하고 예측하는 데 사용한다. 여기서 종속 변수는 예측하려는 변수로 일반적으로 출력값이고, 독립 변수는 종속 변수에 영향을 주는 변수로 입력값이다. 즉, 선형 회귀는 입력값과 출력값 간의 관계를 선으로 정의하고, 선을 통해 다음 입력값에 대한 출력값을 예측하는 것을 말한다.

1-2. 예시

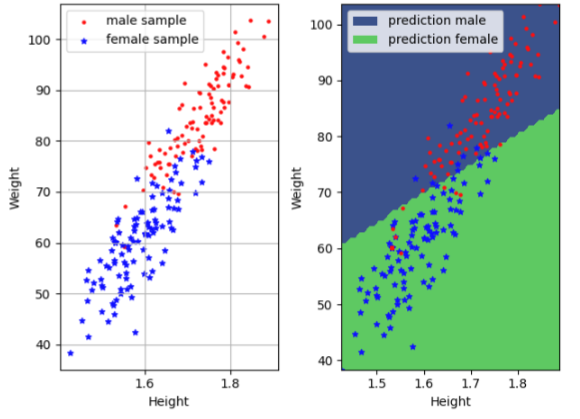
  선형 회귀의 예시로 키와 몸무게 쌍의 데이터를 통해 남녀 성별을 예측하는 것이 있다. 아래 그림의 왼쪽 그래프를 보면, 남녀 간의 키 몸무게 쌍의 값이 두 가지 영역으로 구분될 수 있는 것을 볼 수 있다. 선형 회귀는 오른쪽 그래프처럼 입력받았던 키, 몸무게 쌍을 통해 남녀 성별을 예측할 수 있는 선을 긋고, 다음 입력값이 어느 영역에 속하느냐에 따라 해당 값의 성별을 예측하는 것이다.

그림 1. 키와 몸무게 쌍과 성별 간의 선형 회귀 예시

#2 모델

2-1. 수학적 정의

  수학적 측면에서 선형 회귀는 아래와 같은 식으로 나타낼 수 있다. 다음 식에서 Y는 예측값, x는 입력값, w는 가중치이다.

그림 2. 선형 회귀 수학적 정의

 

  위의 정의에서는 하나의 가중치가 사용되고 있지만, 실제 모델에서는 여러가지 특성이 고려될 수 있어야 한다. 따라서 여러 가지 특성을 고려하는 특성 함수를 정의하고, 각각의 특성에 대한 가중치를 정의하는 것이 선형 회귀에서는 중요하다. 선형 회귀의 학습은 가중치와 편향을 찾고, 실제값과 예측값의 오차를 가장 적게하는 것을 목표로 한다.

2-2. 손실 함수 (Loss function)

  손실 함수는 예측값과 실제값의 오차를 나타내는 함수이다. 손실 함수의 정의는 예측값에 실제값을 뺀 후 제곱하여 입력값의 개수만큼을 나눈 것이다. 제곱을 하는 이유는 오차를 항상 양수만 사용하여 절대값이 모델로부터 얼마나 벗어나는 지를 비교하고, 손실 함수를 통해 최적의 가중치를 찾을 때 미분을 사용하여 기울기가 0인 점을 찾기 위해서이다. 이에 따른 손실 함수의 수학적 정의는 아래와 같다.

그림 3. 손실함수의 수학적 정의

그림 4. 손실 함수 그래프

 

  위의 손실함수의 정의는 모든 오차를 동일하게 취급하는 평균제곱오차(MSE) 방식의 정의이다. 이외에도 오차를 표현하는 함수는 다양한 방식(평균 절대 오차, 평균 제곱근 오차, 평균 제곱 로그 오차, 후버 손실 등)이 있다.

2-3. 최적화 (Opimization)

  모델의 오차를 최소화 하기 위해, 가중치에 따른 손실함수를 최솟값을 찾아야 한다.

경사하강법

  경사하강법은 함수의 최솟값을 찾는 방법으로 손실함수에서도 최솟값을 찾기 위해 사용되기도 한다. 경사하강법은 초기에 임의의 점을 선택하고, 편미분을 통해 점의 기울기를 찾는다. 이후 기울기의 반대 방향으로 이동하며 최솟값을 찾는다. 점을 이동할 때는 학습률이라는 하이퍼 파라미터를 이용하여 얼마나 큰 단계로 이동할 지 선택할 수 있으며, 충분한 반복을 통해 최적점에 수렴하게 된다. 하지만 학습률이 너무 크거나 작은 경우 수렴하지 못 하기 때문에 학습률을 잘 설정하여야 한다.

그림 5. 경사하강법 수학적 정의

그림 6. 경사하강법 그래프

 

  경사하강법은 크게 세 가지 종류가 있으며 다음과 같다.

• (Full) batch gradient descent: 전체 데이터에서 기울기를 계산
• Mini-batch gradient descent: 데이터의 서브셋에서 기울기를 계산
• Stochastic gradient descent: 하나의 샘플에서 기울기를 계산

학습률

  앞서 말한 것처럼 학습률을 설정하는 것은 중요하다. 이를 최적화 하는 학습률 조절 알고리즘들은 다음과 같다.

• Adagrad (Adaptive Gradient Algorithm): 과거의 그래디언트를 보존하여 학습률을 조절하는 방식, 학습이 진행됨에 따라 이전 그래디언트의 제곱값을 누적하여 학습률을 조정, 이는 각각의 매개변수에 대해 개별적으로 학습률을 조절하여 자주 등장하지 않는 특성에 대해서는 큰 학습률을 적용하고 자주 등장하는 특성에 대해서는 작은 학습률을 적용하는 효과를 가져옴, 그러나 학습이 진행됨에 따라 누적된 제곱 그래디언트가 너무 커지면 학습률이 매우 작아져서 학습이 멈출 수 있음
• RMSprop (Root Mean Square Propagation): Adagrad의 한계를 극복하기 위해 제안된 방법, 누적된 제곱 그래디언트의 평균을 사용하여 학습률을 조절, 이전 그래디언트의 제곱값을 지수 이동 평균을 사용하여 계산하여 학습률을 조정, 이를 통해 Adagrad보다는 더 안정적으로 학습
• Adam (Adaptive Moment Estimation): 모멘텀 최적화와 RMSprop을 결합한 방법으로, 각 매개변수마다 학습률을 조정, 지수 이동 평균을 사용하여 그래디언트와 그래디언트의 제곱값을 추정하고 이를 사용하여 매개변수를 업데이트, 모멘텀 방법을 통해 관성을 고려하여 이전 그래디언트의 영향을 조절, Adam은 다양한 문제에서 효과적으로 작동하며 많은 딥 러닝 모델에서 기본 최적화 알고리즘으로 사용

3. 구현

귀찮다... 언젠간 업로드 함